This section contains works-in-progress, preliminary results and open questions. Feel free to contact me and comment.
June 26, 2021 - Challenging the Photon Clock
The photon clock
The concept of time dilation, time running slower for moving objects, was first proposed by Albert Einstein [1] after the observation that the speed of light is independent of the velocity of an observer with respect to any stationary frame of reference. The popular derivation in the years after typically involves an imaginary ‘photon clock’, two parallel mirrors between which a photon bounced up and down. The time interval for one full cycle of the photon was set at 𝛥t. If this photon clock moves with respect to the stationary observer, the simple fact that the observed speed of light may not change requires that the observed frequency of the photon clock decreases. In other words, time slows down for the photon clock because it moves. The derivation for how much the clock slows down is one of the most famous parts of Special Relativity and can be found everywhere, but we will briefly repeat it here. See Figure 1.
Figure 1. Einstein’s photon clock.
The green arrows show the path of the photon as observed by the stationary observer in the case the clock is standing still (left) or moving with a velocity v (right). Note that both arrows have the same length, because the observed velocity of the photon should always be equal to c. The photon is at the bottom of the clock at t = 0. When the clock is standing still, the observer sees the photon reaching the opposite side of the clock at t = 𝛥t/2. When the clock is moving at uniform velocity v, it will traverse the same distance, but no longer vertically upwards, but under an inclined path. By using Pythagoras’ Theorem it is readily found that the vertical velocity as observed by the stationary observer is equal to √(c² - v²). As a result, the apparent time retardation is proportional to c and this vertical velocity, or 𝜸 = c/√(c² - v²) = 1/√(1 - v²/c²).
Inconsistencies of the photon clock
Simple and elegant as this derivation of time dilation may seem, there are two problems with the photon clock. In the first place, the Platonic Theory of Relativity denies the existence of photons and considers electromagnetic radiation as a wave phenomenon only, including a medium of propagation. This means that the photon clock cannot be used. Instead, one could consider an optical resonator cavity, consisting of two concave mirrors of appropriate curvature and distance, similar to the ones used in laser systems. Such a laser cavity could be used as the analogy of the photon clock, however, this does not solve the problem. When such a laser cavity contains any electromagnetic field in resonance, displacing the clock sideways will not drag the radiation along. When the clock moves, certainly at relativitic velocities, you effectively remove the mirrors from the optical cavity so that the radiation field will escape (note that the same argument could also be brought up for the photon clock). Rotating the optical cavity by 90 degrees, so that it moves in the longitudinal direction, will not solve this problem either. At relativistic velocities it will not be possible to maintain a stable optical self-resonance mode, because the mirror curvatures will never match the diffraction of the electromagnetic field.
Figure 2. Schematic of an optical resonator, containing light between two concave mirrors. In order for such a resonator to be stable, the radius of both mirrors must accurately match the radiation diffraction. If the mirrors would move at relativistic velocities in longitudinal direction, the radiation would hit one mirror too early and the other too late, so that the cavity will be out of alignment and the radiation escapes.
Conclusion
In conclusion, the photon clock describes a situation that will never occur in physical reality. Therefore, it should not bebe used to describe the effect of time dilation. Indeed, the originial paper by Einstein [1] deals with the issue much more caution.
References
[1] Einstein A. (1905); "On the electrodynamics of moving bodies”. Annalen der Physik, 17(1905), pp. 891-921.
June 27, 2021 - Time Management
The Relativistic Train and the Tunnel
A well-known and fascinating example of the consequences of the Special Theory of Relativity is to describe what happens when a train, longer than the length of a tunnel, passes through that tunnel at relativistic speed. It is assumed that the speed of the train is so high that the Lorentz-contracted length of the train is shorter than the tunnel. As a result, an observer stationary with respect to the tunnel will see the end of the train go into the tunnel before the front of the train comes out at the other side (the train is shorter than the tunnel). An observer inside the train, however, will see the front of the train come out of the tunnel before the end of the train goes in (the train is longer than the tunnel).There is a nice animation on YouTube that describes the whole thing according to scientific consensus.
This can be elegantly depicted by the Simple Theory of Relativity too, as shown below.
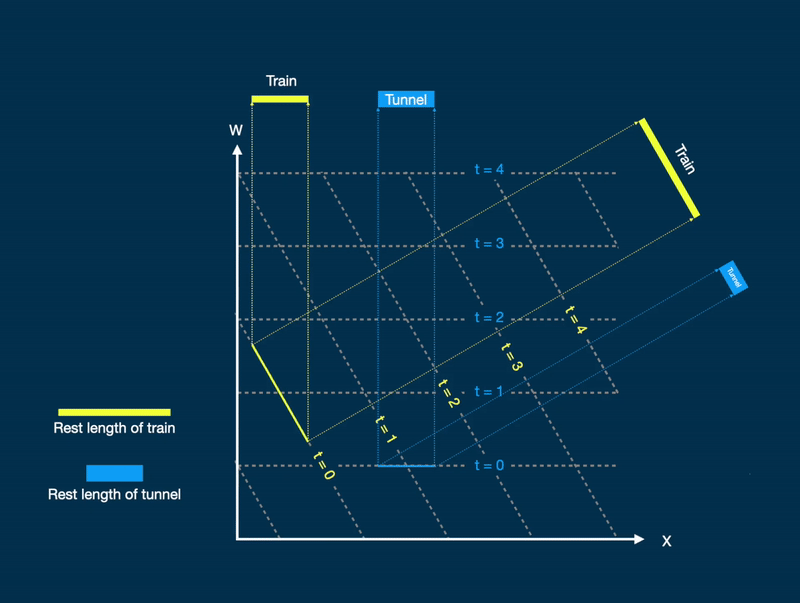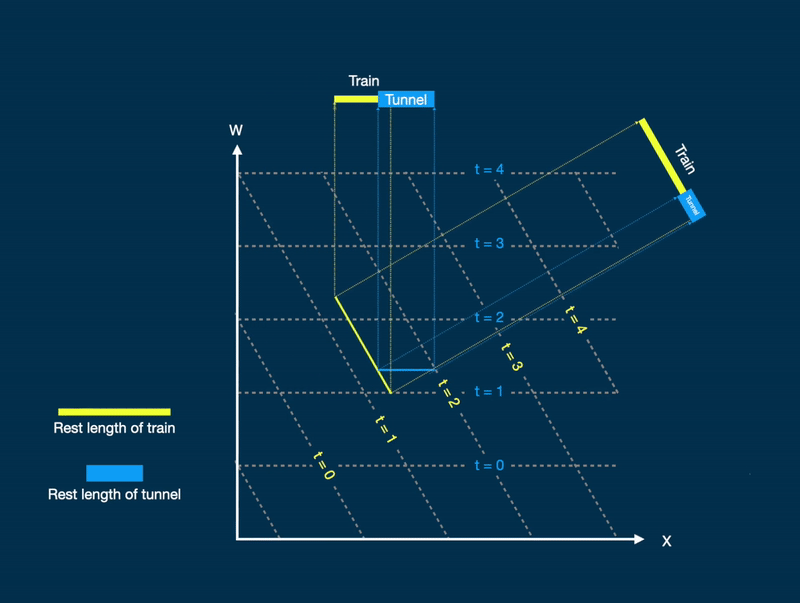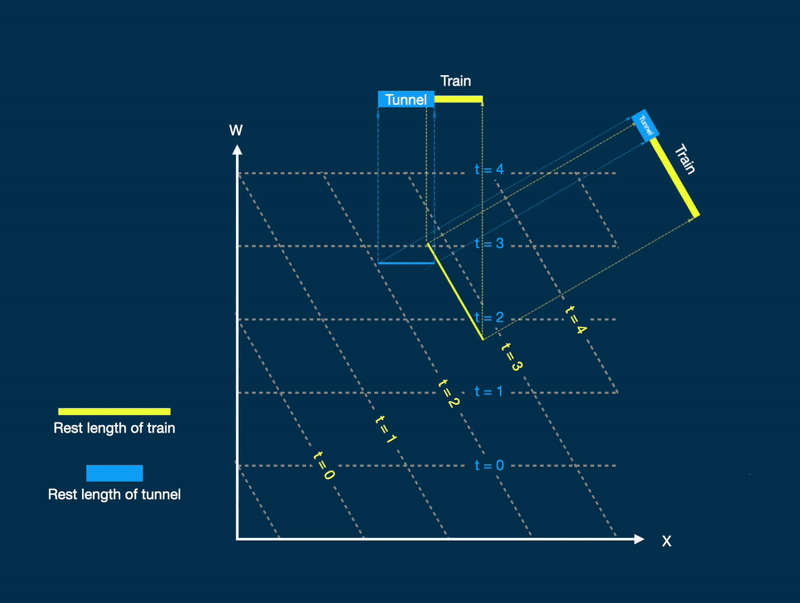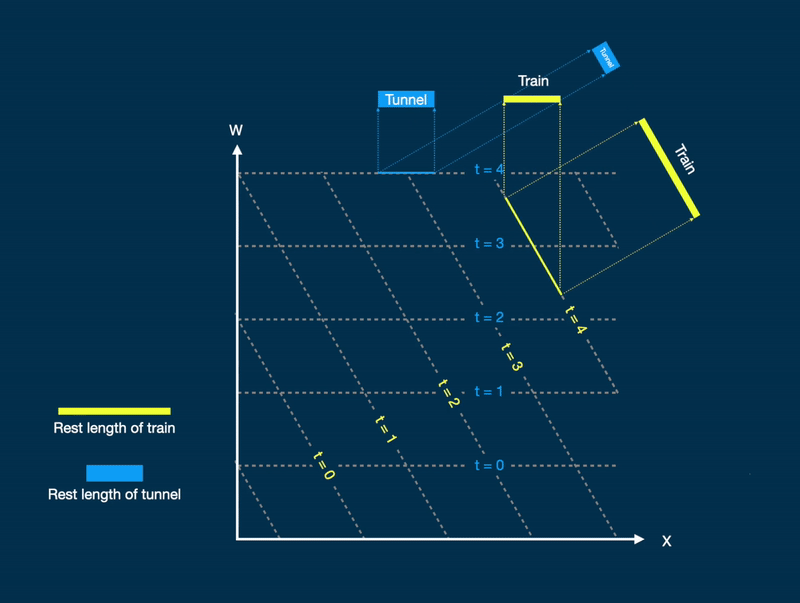
Figure 3. A 4-dimensional space showing a train (yellow) with rest length longer than a tunnel (blue) which fits exactly inside the tunnel at a relativistic speed when observed from the frame of the tunnel (projection on top). When observed from the frame of the train (rotate image 60 degrees counter clockwise) this is not the case.
Timing problems
The story of the relativistic train becomes really interesting when the ends of the tunnel are both closed at the moment the train is inside the tunnel (as seen from the frame of the tunnel). Because seen from the train the tunnel is shorter than the train, an observer inside the train will not see both ends of the tunnel close simultanesously, instead he sees one end close first (before the front of the train reaches the end of the tunnel) and the other end later (at the moment the end of the train is inside the tunnel. In order to understand how this is explained by the Simplified Theory of Relativity, we first have to look at the concept of simultaneity, or the lack thereof. See Figure 4.
Figure 4. Seen from the train the left hand side of the tunnel is at an earlier time (time as experienced by the train) than its right hand side.
The train (yellow in Figure 4) has a rest length of M0, whereas the tunnel (blue) has a rest length of L0. The 3D perception of an observer in rest with respect to the tunnel is shown on top of Figure 4. The projected length of the tunnel is the same as its rest length, but the projected length of the train is shorter and is equal to M0 cos(𝜑) = M0/𝛾. As a result, the observed length of the train is identical to the observed length of the tunnel. Seen from the train the perception is different, which is shown in the projection at the top right of Figure 4. The projected length of the train is now equal to its rest length M0, whereas the projected length of the tunnel is contracted to L = L0 cos(𝜑) = L0/𝛾. Clearly, according to an observer inside the train the train will never fit inside the tunnel.
Now look at the positions and orientations in the 4D space, in the center of Figure 4. The yellow line segment represents the train, the blue line segment represents the tunnel. Both move at velocity c through 4D space with an angle 𝜑 between their velocity vectors. For an observer inside the train the tunnel extends over a distance 𝝙x in his direction of motion through 4D space. According to the Simplified Theory of Relativity the observer cannot perceive this distance in space, however, this distance does relate to his perception of time. In fact, the observer will travel a distance 𝝙x in a time 𝝙x/c. With 𝝙x = L0 sin(𝜑) we find that 𝝙x= L0v/c, so that the time it takes an observer i the train to travel the distance 𝝙x amounts to 𝝙t = L0v/c2. As seen earlier, the perceived length of the tunnel, according to the observer in the train, amounts to L = L0 cos(𝜑) = L0/𝛾, so that L0 = 𝛾 L so that
𝝙t = 𝛾Lv/c2.
This is indeed the familiar expression for time separation according to the Special Theory of Relativity.
Time according to the PTR
My current idea about the concept of ‘time' is simply that matter is flying in the 4D universe through a grid of ether particles. On a subatomic level, there is an interaction between the ether particles and elementary particles of matter. So an electron does not jump to a lower energy level by releasing a photon, instead, it puts an ether particle back into the grid. Or it steals another ether particle from the grid and jumps to a higher energy level. These interactions can only take place when the ether particles move with respect to matter, which they do by definition. If matter were not moving, no interaction would be possible and time would stand still. So rather than direct energetic interactions between different atoms, the Simplified Theory of Relativity introduces an 'energy bank’, which is the ether, and which acts a mediator when elementary particles exchange energy.
Will be continued…
[1] Challenge to the Special Theory of Relativity, Xinhang Shen, Physics Essays 29(1):142-148.